출처: 만들면서 배우는 생성 AI, 데이비드 포스터
확산 모델은 GAN과 함께 최근 AI 기술 중 많은 관심을 받은 개념이라고 한다.
확산 모델은 여러 벤치마크에서 GAN 보다 우수한 성능을 보이며, CV쪽에서 활발히 사용된다고 한다.
5.1 아이디어


Diffusion model의 기본 원리를 TV 매장으로 비유한 소개글이지만, 정말 설명을 못하는 것 같다.
어쨌든 이러한 아이디어가 확산 모델의 기본 개념을 나타낸다. 여러 노이즈에 노출된 후, 학습이 진행됨에 따라 노이즈를 제거하여 최종적으로는 진짜 같은 영상(이미지)를 생성하는 것 같다.
5.2 잡음 제거 확산 모델
잡음 제거 확산 모델의 기본 개념은 위 TV의 아이디어와 유사하다.
연속해서 이미지 속에서 노이즈를 없애는 것이다.(없애도록 훈련 시키는 것)
확산 모델에서는 정방향 (잡음 추가)과 역방향 (잡음 제거)가 존재한다고 함!
5.3 정방향 확산 과정

위 그림을 통해서 정방향 확산 과정 (노이즈 추가)을 알아보자.
x0을 계속해서 손상시켜 Xt로, 즉 랜덤한 가우스잡음과 동일하게 만든다고 가정해보자.
이렇게 하려면 어떻게 해야할까?
위 그림 Xt-1 이미지에 분산 Bt를 갖는 약간의 가우스 잡음을 추가하여 이미지 Xt를 생성하는 함수 q를 정의할 수 있다.
이 함수를 계속 적용하면 계속해서 노이즈가 커지는 이미지 시퀀스를 만들어낼 수 있는 것이다.
업데이트 과정을 수식으로 표현하면 다음과 같다.

결론: 정방향 확산 과정은 input된 이미지를 완전한 노이즈로 바꾸기 위해 계속해서 일정한 분산을 갖는 노이즈를 추가시킴.
5.3.1 재매개변수화 트릭
위에서는 그럼 계산을 T번 해야하는 건가? T번 계산하지 않고 input이미지에서 바로 최종 이미지(잡음 낀 이미지)로 건너뛸 수는 없을까?
이를 위해 재매개변수화 트릭이라는 개념이 등장한다.

수식의 두 번째 줄 (xt = √at * xt-1 ~ ) 이 줄은 두 개의 가우스 분포를 더하여 새로운 가우스 분포 하나를 얻을 수 있다는 사실을 이용한다. 따라서 원본 이미지에서, 최종 뿐 아니라 어떠한 단계로든 이동할 수 있다!
또한, 원래 Bt대신 표본at를 사용하여 확산 스케쥴을 정의할 수 있다.
표본 at는 신호(원본 이미지)로 인한 분산이고, 1-표본at는 잡음으로 인한 분산이다.
따라서 정방향 확산 과정 q는 다음과 같이 쓸 수 있다.

5.4 확산 스케쥴
또한 각 타임 스텝마다 다른 Bt를 자유롭게 선택할 수 있다. 즉, 모두 동일할 필요가 없다는 것이다!
이처럼 Bt값이 t에 따라 변하는 방식을 확산 스케쥴이라고 한다.
(원래 논문에서 저자들은 Bt에 대해서 선형 확산 스케쥴이라고 했다고 한다.)
{Bt가 B1=0.0001에서 Bt=0.02까지 선형적으로 증가되기 때문}
이렇게 하면 잡음 추가하는 과정에서 초기 단계에서 나중 단계보다 노이즈가 적게 추가된다.
(나중 단계는 거의 노이즈 상태이기 때문!)

확산 스케쥴은 선형, 코사인, 오프셋 코사인 대표적으로 이 세가지로 나뉘고, 위 그림을 통해 각각의 특징을 보자.
코사인 확산 스케쥴 (초록) 에서 잡음이 더 느리게 상승하는 것을 볼 수 있다.
5.5 U-Net 잡음 제거 모델
이제 본격적으로 확산 모델을 사용해보자.
출력과 입력의 크기가 같아야할 때는 U-Net이 유용하므로, U-net을 이용하여 구조를 만들어보자.
noisy_images = layers.Input(shape=(64,64,3)) # 잡음 제거하려는 이미지
x = layers.Conv2D(32, kernerl_size=1)(noisy_images) # Conv2D 통과하면서 채널 수 증가
noise_variances = layers.input(shape=(1,1,1)) # 두 번째 입력은 잡음의 분산(스칼라)
noise_embedding = layers.Lambda(sinusoidal_embedding)(noise_variances) # 사인파 임베딩을 통해서 인코딩 됨
noise_embedding = layers.UpSampling2D(size=64, interpolation = 'nearest')(noise_embedding)
x = layers.Concatenate()([x, noise_embedding])
skips = []
x = DownBlock(32, block_depth = 2)([x, skips])
x = DownBlock(64, block_depth = 2)([x, skips])
x = DownBlock(96, block_depth = 2)([x, skips])
x = ResidualBlock(128)(x)
x = ResidualBlock(128)(x)
x = UpBlock(96, block_depth = 2)([x, skips])
x = UpBlock(64, block_depth = 2)([x, skips])
x = UpBlock(32, block_depth = 2)([x, skips])
x = layers.Conv2D(32, kernerl_size=1, kernel_initalizer='zeros')(x)
unet = layers.Conv2D(3, kernel_size = 1, kernel_initializer='zeros')(x)
unet = models.Model([noisy_images, noise_variances], x, name='unet')코드 네 번째 줄의 사인파 임베딩이 뭘까??
'딥 러닝 > 생성형 AI' 카테고리의 다른 글
| 04. 적대적 생성 신경망(GAN) (0) | 2024.04.06 |
|---|---|
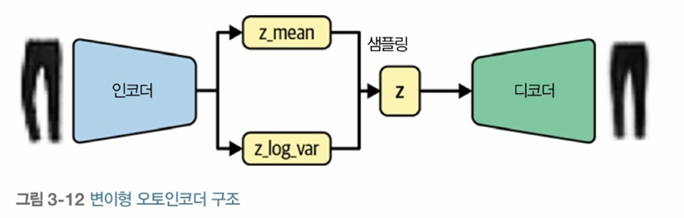
| 03. 변이형 오토인코더 (2) | 2024.03.22 |
| 02. 딥러닝 (1) | 2024.03.17 |
| 01. 생성 모델 (2) | 2024.03.11 |