오늘은 5장인 DFS/BFS + 프로그래머스 한 문제를 풀어보자.
01. 프로그래머스의 "가장 큰 수"

보고 든 생각은 자릿수 비교였다.
각 원소의 가장 앞자리수가 큰 수가 앞에 옴 -> 같을 경우 두 번째 자릿수 비교 -> 반복...
하지만 예시처럼 3과 30/ 3과 34의 비교는 어떻게 될까?
간단하게 3,30,34만 주어졌다고 가정하면 답은 34330이다.
예시와 같이, 원소가 한자리 수 일경우 두 번째 자릿수는 33,44,55와 같이 한 자리수와 같은것으로 간주해도 될 것 같다.
-> 구현하기에 너무 빡세서 그냥 경우의 수로 비교
이제 이를 코드로 짜보았다.
1. 일단 무식하게 버블 정렬 형태로 각 원소의 가장 큰 자릿수를 비교 # str(numbers[j][0] 형태로
2. 만약 numbers[0]이 서로 같다면 -> numbers[j] + numbers[j+1] < numbers[j+1] + numbers[j] 이런 형태로 비교
def solution(numbers):
n = len(numbers)
for i in range(n):
for j in range(0, n-1-i):
if str(numbers[j])[0] < str(numbers[j+1])[0]:
numbers[j], numbers[j+1] = numbers[j+1], numbers[j]
# 만약, 일의 자리수가 같다면-> 다음 자리수를 비교해야함
elif str(numbers[j])[0] == str(numbers[j+1])[0]:
if str(numbers[j])+str(numbers[j+1]) < str(numbers[j+1])+str(numbers[j]):
numbers[j], numbers[j+1] = numbers[j+1], numbers[j]
ans = ''.join(map(str, numbers))
return ans테스트케이스는 통과했지만, O(N^2)이라서 (input은 100,000까지) 틀렸다ㅠ

이중 for문 쓰지말고 어떻게 푸냐..
내가 생각한 자릿수 비교
1. 3vs30 -> 3이 커야함.
2. 878vs87 -> 878이 커야함
3. 454vs45 -> 45가 커야함
-----------------------------------------
-> 문자열 자릿수 비교를 이용 -> 문제: 3vs30을 30이 크다고 인식함 -> 해결: str(list)*4 해버리자
[ 3, 30 ] *4 -> 3333vs30303030 -> 3이 큼!
# 예외처리 -> 모든 숫자 0일경우 -> '000000'이 아닌 '0'만 출력해야함.
def solution(numbers):
numbers = list(map(str, numbers))
def my_key(x):
return x * 4
numbers.sort(key = my_key, reverse=True)
numbers= ''.join(numbers)
# 예외 처리 -> 모든 숫자 0일 경우?
if numbers[0] == '0':
return '0'
return numbers이코테 Ch.5
대표적인 탐색 알고리즘으로 BFS/DFS가 있고, 자주 나오므로 꼭 알아두자.
그전에!!!!!!
가장 기본적인 스택/큐를 복습하고 가보자.
스택
- 박스 쌓기를 생각 (후입선출)
- append()와 pop()으로 별도 라이브러리 없이 구현가능하다
pop() -> 가장 뒤쪽의 데이터를 꺼내오는 함수
큐
- 입장 대기 줄 (선입선출)
- deque.append()와 deque.popleft()으로 deque import해야함
from collections import deque
queue = deque()
queue.popleft()
popleft() -> 가장 앞쪽의 데이터를 꺼내오는 함수
재귀 함수
DFS/BFS를 구현하려면 재귀함수도 이해하고 있어야한다.
피보나치/팩토리얼 같이 자신을 다시 호출하는 함수이다.
-> 종료 조건을 까먹지말자.
DFS (Depth First Search)
깊이 우선 탐색이라고 하며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
그래프는 노드(Node / vertex)와 간선(Edge)로 표현되며,
그래프 탐색이란 하나의 노드를 시작으로 다수의 노드를 방문하는 것을 말한다.
두 노드가 간선으로 연결되어 있는 경우는 '인접하다(Adjacent)'라고 한다.
이 인접하다는 개념을 이용해서, 인접 행렬/ 인접 리스트에 대해서도 알아보자.
인접 행렬: 2차원 배열로 그래프의 연결관계를 표현하는 것
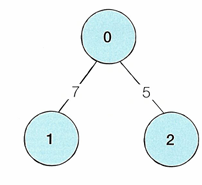

인접 리스트: 리스트로 그래프의 연결 관계를 표현하는 방식
(=> 연결 리스트로 구현하는데, Python의 경우 C++과 다르게 별도 라이브러리 필요가 없다.)
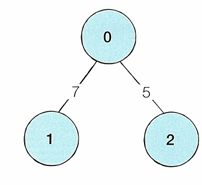

인접 행렬 vs 인접 리스트
-> 메모리 측면: 인접 행렬은 모든 관계를 저장하므로 메모리 측면에서 비효율
인접 리스트는 연결된 정보만을 저장하므로 효율적
하지만 이 때문에 인접 리스트는 특정 두 노드의 연결 여부 정보를 얻는 속도가 느림 (하나하나 확인해야해서)
((((만약 노드 1과 2과 연결 되어 있는 지가 궁금하다면
인접 행렬의 경우 graph[1][2]만 하면 바로 나오지만,
인접 리스트의 경우 앞에서부터 차례대로 확인해야 함!))))
다시 앞으로가서 DFS는 깊이 우선 탐색 알고리즘이라고 했다.
DFS는 특정 경로로 탐색하다가 특정한 상황에서 최대한 깊숙이 노드를 방문 한 후 다시 돌아가 다른 경로를 탐색하는 알고리즘이다.
구체적인 동작 과정은 아래와 같다.
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 있다면 그 인접노드를 스택에 넣고 방문 처리를 한다.
방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다. - 2번의 과정을 더이상 수행할 수 없을 때까지 반복한다.
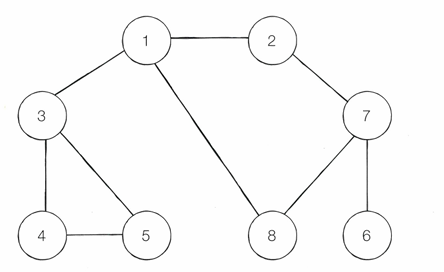
이 그림을 예시로 들어보면, DFS 과정은 아래와 같다,
[노드 방문 순서]
1 -> 2 -> 7 -> 6 -> 8 -> 3 -> 4 -> 5
스택의 흐름:
1: 1
2: 1, 2
3: 1,2,7
4: 1,2,7,6
5: 1,2,7 (6pop)
6: 1,2,7,8
7: 1,2,7 (8pop)
8: 1,2 (7pop)
9: 1 (2pop)
10: 1,3
11: 1,3,4
12: 1,3,4,5
이제 DFS를 코드로 구현해보자.
(힌트 : 스택/재귀함수를 활용해서)
# 힌트: 재귀 + 스택 활용해서 구현하기기
def dfs(graph, v, visited): # graph;연결리스트, v;노드, visited;방문한 노드들을 표시하는 리스트
visited[v] = True # 현재 노드를 방문처리
graph = [
[], # 편한 인덱싱을 위해서 0은 비워둠
[2,3,8], # 1번 노드 = 2,3,8과 연결
[1,7], # 2번 노드 = 1,7과 연결
[1,4,5], # .
[3,5], # .
[3,4], # .
[7], # .
[2,6,8], # 7번 노드 = 2,6,8과 연결
[1,7] # 8번 노드 = 1,7과 연결결
]
visited = [False] * 9 # visited = [False,False,False,...False]'코테 스터디' 카테고리의 다른 글
| Ch4. 구현 (1) | 2025.07.11 |
|---|---|
| Ch3. 그리디 알고리즘 (0) | 2025.06.28 |













