Ch3-2 출력층 설계, 실습
출력층 설계하기
신경망은 분류/회귀 모두 이용할 수 있고, 어떤 문제냐에 따라서 출력층에서 사용하는 활성화 함수가 달라진다.
일반적으로 회귀문제에는 항등 함수를, 분류문제에서는 소프트맥스함수를 사용한다.
번외로)
시그모이드 vs 소프트맥스의 특 ----->소프트맥스(=다중분류), 시그모이드 (=이진분류)

그리고
일반적인 DNN과 CNN에서는 주로 ReLU를 ,
RNN에서는 주로 시그모이드와 하이퍼볼릭 tan함수를 사용한다고 한다.
다시 책으로 돌아와서, 항등함수와 소프트맥스 함수를 구현해보자.
항등함수란 중학교 때 배웠다시피 입력=출력이 같은것을 말한다.
한편 소프트맥스 함수는 다음과 같다.
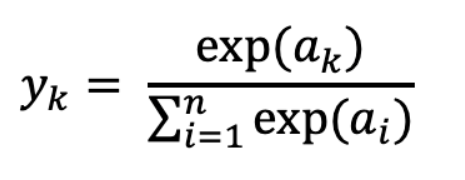
exp(x) = e^x인 지수함수.
그림으로 나타내면 아래와 같다.

Output인 y1, y2, y3를 보면 모든 입력에서 영향을 받는다는 것을 알 수 있다.
이를 구현해보면,
a = np.array([0.3, 2.9, 4.0])
exp_a = np.exp(a)
print(exp_a)
[ 1.34985881 18.17414537 54.59815003]sum_exp_a = np.sum(exp_a)
print(sum_exp_a)
74.1221542101633y = exp_a / sum_exp_a
print(y)
[0.01821127 0.24519181 0.73659691]
함수식을 구현해보면,
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
소프트맥스 함수 구현 시 주의점
-오버플로우 문제
소프트맥스 함수는 지수 함수를 사용한다. 공식을 자세히 보면, 지수함수끼리 나눗셈을 하는데, 이런 큰 값끼리 연산을 하게 되면 값이 매우 불안정해진다. 이 오버플로우 문제를 해결하기 위해 수식을 개선해보자.

1: 분자 분모에 C를 곱하고, 2: 이 C를 괄호 안으로 옮겨서 로그로 만든다. 3: logC = C'로 치환
이렇게 수식을 바꾸면 지수함수를 계산할 때 어떤 정수를 더해도(빼도) 결과는 바뀌지 않는다는 것이다.
또한 위 수식에서 C'에 어떤 값을 대입해도 상관없지만, 통상적으로는 입력 신호 중 최대값을 이용한다.
a = np.array([1010, 1000, 990])
np.exp(a) / np.sum(np.exp(a))
array([nan, nan, nan])값이 너무 크기 때문에 Nan이 출력되는것을 볼 수 있다.
c = np.max(a)
a - c
array([ 0, -10, -20])위 그림은 +로 되어있지만 사실상 오버플로우 대책은 -로 해줘야한다!! (값이 너무 작으면 더하기)
np.exp(a - c) / np.sum(np.exp(a-c))
array([9.99954600e-01, 4.53978686e-05, 2.06106005e-09])
따라서 오버플로우를 방지한 개선된 소프트맥수 함수는 다음과 같이 구현할 수 있다.
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
소프트맥수의 출력값의 의미
우리는 위 수식을 통해 소프트맥스 함수가 항상 0~1로 출력되는것을 확인했다.
또한 소프트맥스함수는 주로 분류일 때 사용된다고 했으므로, 출력값을 확률의 개념이라고 생각할 수 있다.
+ 출력층이 여러개이므로 각각의 값 = 각각 정답일 확률을 표현한 것
마무리)
지금까지 그림과 식들을 통해 입력 데이터를 기반으로 입력층에서 출력층까지 변수들이 이동하는 것을 살펴보았다.
바로 위의 문장을 순전파 ( forward propagation )이라고 한다.
이제 MNIST 데이터셋으로 간단한 실습을 해보자.
MNIST란 손글씨 이미지 데이터 모음으로, 학습용 데이터로 매우 적합하다.
import sys, os
sys.path.append(os.pardir)
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) =\
load_mnist(flatten=True, normalize=False)
print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)
(60000, 784)
(60000,)
(10000, 784)
(10000,)위의 코드에서 normalize=True 는 픽셀값을 0~1 사이 값으로 정규화 할지 말지 결정하는것을 의미한다.
두번 째 인수인 Faltten은 입력이미지를 1차원으로 바꿀지 말지를 결정합니다. (False는 3차원 배열로)
이제 이미지를 출력해보자.
from PIL import Image
def img_show(img):
pil_img = Image.fromarray(np.unit8(img))
pil_img.show()
(x_train, t_train), (x_test, t_test) = \
load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label)
print(img.shape)
img = img.reshape(28, 28)
print(img.shape)
img_show(img)
주의사항으로, flatten=True로 설정한 이미지는 1차원 배열로 저장되어있다.
따라서 이미지를 표시하기 위해서는 28x28크기로 reshape(-1,28,28)해야한다!!
신경망의 추론 처리
위에서 구현한 신경망은 입력층 뉴런 784개( 28x28 ), 출력층 뉴런은 10개 (0~9를 분류)임을 확인할 수 있다.
또한, 여기서 은닉층을 두 개 설정할 것이고, 각각 50개, 100개의 뉴런을 배치해보자.(임의로 정한것)
def get_data():
(x_train, t_train), (x_test, t_test) =\
load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
W1,W2,W3 = network['W1'], network['W2'], network['W3']
b1,b2,b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a1)
a3 = np.dot(z2, W3) + b3
y = softmax(a3)
return y이제 모델의 정확도를 구하는 원리를 알아보자.
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p = np.argmax(y) # 확률이 가장 높은 원소의 인덱스를 얻는다.
if p == t[i]
accuracy_cnt += 1
print("Accuracy: " + str(float(accuracy_cnt) / len(x)))
Accuracy: 0.935293.52%의 정확도를 나타낸다.
MNIST 데이터셋을 얻고 네트워크를 생성한다.
이어서 for문을 돌며 x에 저장된 사진을 한장 씩 꺼내서 predict()함수에 집어 넣는다.
predict() 함수는 각 레이블의 확률을 넘파이 배열로 반환한다.
예를 들어 [0.1, 0.8, 0.9 .... 0.1] 같은 배열이 반환되며 이는 각각이 인덱스(숫자 번호)일 확률을 나타낸다.
그 다음 np.argmax()함수로 이 배열에서 값이 가장 큰 ( 확률 제일 높은) 원소의 인덱스를 구한다.
이것이 바로 예측 결과 !
마지막으로 정답 데이터와 비교하여 맞힌 숫자를 count += 1씩 하고, count / 전체 이미지 수 로 나눠서 정확도를 구하는 것이다.